YouTube Video - The Real Hustle - Rigged Dice Ripoff

YouTube Video - The Real Hustle (UK) - Casino Dice Scams

Craps for Profit: The Math of Dice Control

Craps for Profit: The Math of Dice Control

By Dan Pronovost

Dan Pronovost is the owner and president of DeepNet Technologies, makers of a wide range of gambling training products and software. Their web sites are: www.HandheldBlackjack.com and www.SmartCraps.com and all products are available for free trial download. Dan is the creator of the new card counting system Speed Count, which is being taught by Henry Tamburin and Frank Scoblete in the Golden Touch Blackjack two day courses: www.GoldenTouchBlackjack.com.

Can anyone make money playing Craps?!

Some readers of Blackjack Insider may know me for my company's blackjack training products (www.HandheldBlackjack.com), and other works in the statistical study of blackjack. Well, we embarked last year into a new area of gambling, and after spending over a year researching, developing and writing, we have just launched a new software product: Smart Craps (for Windows). Smart Craps is based on brand new mathematical methodologies, designed to answer with statistical and scientific clarity, the infamous question plaguing advantage craps players everywhere:

"Can anyone honestly get an edge over the casino playing craps?"

Before I answer this question (in this, and a continuing series of upcoming articles), let me start by saying that this is a very controversial subject, and will raise the shackles of many 'experts' (maybe even you, fine reader!). But before you judge too quickly, please be fair, and read the analysis presented here, and to be continued in future newsletters. Smart Craps, and the ideas it uses, are new. Nobody has looked at dice control from the perspective we use, and with the rigorous statistical approach we've applied.

So� to answer this question (and lay down them fightin' words): yes, craps is a beatable game, provably with statistical certainty, in the hands of the skilled dice controller. Flipping the coin for a moment, there will no doubt be some readers who play advantage craps already whose response would be, "Duh� I've known that! Been winning for years!" But winning, and proving you are winning with statistical relevance, are two different things. And, as this series of articles will reveal, Smart Craps will show that most dice controllers are not playing optimally, or even worse, think they are playing with an advantage and are not doing so. Smart Craps is much more than just a proof: it is a software tool to help dice controllers maximize their edge, tune their game, and learn what edge is possible.

Jumping ahead�

These ongoing articles will be 'stand alone', meaning that you do not need to use or have the Smart Craps software to understand or follow along. But for the curious, or those who want to jump ahead, you can download the software from:

www.SmartCraps.com/SmartCrapsInst.exe

Just download this exe, save it on your Windows computer, and run it. The software is shareware, which means you can try it out for free. The documentation is over 100 pages, including everything you need to know and covers basically everything we'll talk about in these articles.

The Theory of Dice Control

This is intended as a brief summary only on dice control and the physical skill of dice setting. If you want to master the physical skill of dice setting, you will want to read and consult with some of the resources at the end of this article. Unlike card counting in blackjack, dice setting is a physical skill, and cannot be mastered through reading and mental practice alone.

Dice setters attempt to control the physical throw of the dice in such a way as to influence the outcome of the dice. This skill, when used consciously at different points in the game, generates a non-random distribution of outcomes, which the shooter hopes reverses the casino's edge in the game to the player's favor. To understand the physics of dice control, let's look at an actual craps table:

Figure 1: Axes of rotation on a craps table

With these labels, we can see that a shooter will be throwing the dice along the X axis toward the end of the table. Generally, a skilled dice setter will hold the dice together, parallel to the Z axis, as shown below:

Figure 2: Throwing the dice parallel to the Z axis of the table

A typical controlled shooter is attempting to cause the dice to rotate only along the Z axis. In theory, any spin in the Y or X axis can introduce unexpected bounces and a less controlled outcome. With a spin in only the Z axis, the outside numbers on the dice set should not occur in the final roll result.

Now that we understand the basic physics of dice control, we can see that the actual dice set is relevant for a skilled shooter. The set determines exactly what numbers are on top and on the sides for both dice. In the above figure, the twos are on top and the fours are on the front. The standard notation used in Smart Craps would describe this dice set as T2F4/T2F4, meaning the two on top and four in front for the left die and right die. The notation T3F5/T3F1 is often called the 3V set in popular texts, for example. Describing the top and front of a die (actually, any two adjacent sides will do) completely determines the values of the remaining sides. The 'T' and 'F' can be dropped, shortening the notation for a set, such as the 3V, to 35/31.

As well as limiting the spin of the dice to the Z axis, extremely proficient controlled shooters also try and fix the rate of spin for both dice to be the same. This can further reduce the dice outcomes for advantage play. For example, with a 22/44 or hard way set (sixes and ones on the outside), a perfectly controlled throw with Z axis rotation only at the same speed for both dice means the outcome should be one of: 22, 33, 44 or 55.

Using a hard way set again, suppose a controlled shooter achieves Z axis control but not rotation rate. In theory, the possible outcomes are the sixteen permutations of the four on-axis sides: 22, 23, 24, 25, 32, 33, 34, 35, 42, 43, 44, 45, 52, 53, 54, and 55. Notice that there are passing outcomes that sum to seven, as well as failures (61, 16). This will come into play when we talk about the statistics of dice setting, and the best way to determine if a skilled shooter is influencing the outcomes.

In the next sections, we discuss two ways of determining if a shooter is in fact influencing the dice outcomes: SRR (Seven to Rolls Ratio) and the new Pro Test© by DeepNet Technologies.

SRR - Seven to Rolls Ratio

Ok� you claim to be an expert dice controller, and making millions at craps. Good for you! Now, how do we prove it, with the same kind of mathematical certainty that we talk about with card counting in blackjack?

The most common statistical analysis of the game of craps to date is the SRR: seven to rolls ratio. This measures the number of seven sums in two dice compared to the other outcomes. If you are a random shooter, you will roll one seven in every six rolls (or, one seven for every five non-sevens). This simple fact can be seen if we look at all possible outcomes for the sum of two dice:

Roll:	2	3	4	5	6	7	8	9	10	11	12
	11	12	13	14	15	16	62	63	64	56	66
		21	31	41	51	61	26	36	46	65
			22	23	24	25	35	45	55
				32	42	52	53	54
					33	34	44
						43
Total:	1	2	3	4	5	6	5	4	3	2	1	= 36

Figure 3: Dice outcomes for a random shooter

The above table for a dice controller will be quite different, but the number we concentrate on is the number of seven outcomes. On the come out roll, we want to maximize the number of sevens (i.e. have the highest possible SRR fraction, or lowest SRR proportion value), and on any point roll we want to minimize the number of sevens (i.e. have the lowest possible SRR fraction, or highest SRR proportion value).

In Smart Craps, we model an SRR shooter by specifying both the minimum and maximum SRR ratio they are capable of achieving. Then, we can devise a betting system that uses the appropriate SRR for different situations (the minimum SRR on come out rolls and the maximum SRR on point rolls).

With the above approach, we can convert various SRR ratios to actual player edges. In Smart Craps, we do this by defining a simulation matching the SRR parameters, and running it for a few million rounds. For example, if we assume the following:

• Shooter uses a controlled throw on the come out roll that minimizes their SRR to 1:5.5.
• Shooter uses a controlled throw on all point rolls that maximizes their SRR to 1:6.5.
• Zero odds game, with flat pass line bets only.
• Player edge: +3.43% (using 100 million craps rounds, where each round is a single bet. 342 million rolls in this case).

While it is possible to determine the player edge mathematically with different SRR values in the case of simple flat pass line bets, things get more complicated when you add unusual bets and rules (vigs, odds, uneven payouts, etc.) Smart Craps makes it possible to determine the true edge empirically with real-world craps scenarios and conditions, using game simulation.

It is interesting to observe that the actual dice set is not relevant when simulating SRR shooters. The SRR is a direct result of their technique and set, not the other way around. But SRR shooters are no different from any dice setter: the principles of axis rotation discussed previously apply.

Also, the actual dice sums, while very relevant to computing player edge, are not directly correlated to the influence the dice setter achieves. For example, if a shooter uses a hardway set, they may still achieve perfect z-axis rotation, not getting an outside six or one to appear, yet a seven is rolled. For example, the outcome 34 and 25 indicate perfect z-axis rotation with a hardway set. Yet, they may fail to get z-axis rotation and still get a seven with a 61 or 16 outcome. This weakens the statistical accuracy of the SRR as a good measure of dice setting skill. SRR is great for computing player edge, but is a weak statistical measure of dice setting skill.

Enter Pro Test©� a fresh look at the statistics of dice setting, and a better mathematical approach to measuring skill and player edge.

Pro Test©: a better dice control metric

We've seen in the previous section that the seven to rolls ratio, while somewhat intuitive and useful for calculating player edge, is not the best possible measure of dice setting skill. This results from the fact that sevens can be both 'good' and 'bad', meaning that they occur when we both achieve and fail z-axis control. This weakens the statistical utility of SRR for determining player dice setting skill.

Let's take a fresh statistical look at dice control, starting with the basic physics principles described in the earlier.

Z-axis rotation

First and foremost, dice setters are trying to limit the dice rotation to the z-axis. This simply means that neither of the outside numbers shows up in the outcome. Hence, there are 4 times 4 = 16 possible outcomes that succeed in rotating in the Z-axis only. With a hardway set, this means each die outcome is one of: 2, 3, 4 and 5.

Secondly, a good dice setter tries to control the number of face rotations or pitches between the two dice when they do achieve z-axis control. Ideally, the two dice leave their hands in perfect symmetry, and rotate equally in the z-axis, bounce off the floor and back, and land with one of four possible outcomes. With a hardway set, this means one of: 22, 33, 44, or 55.

Thirdly, dice setters attempt to try to limit the number of double pitches when they achieve z-axis control. Ideally, the dice land up together (zero face rotations as noted above), or single pitch (are offset by 90 degrees or one rotation). Eliminating double pitches is useful with some dice sets, such as the hardway set: the only seven sums on the z-axis controlled outcomes occur when the dice double pitch (52, 25, 34 and 43). This can be relevant in different points of the game, such as point cycle rolls.

Thinking in practical terms, how do we know if a throw has stayed on z-axis rotation for any given dice set? Or, how do we know how many face rotations or pitches occurred on those successes? While it is very clear with a hardway dice set, other sets will lead to ambiguous results unless the dice are clearly marked (or colored) and the starting dice set recorded. For the purposes of the Pro Test, we always use a hardway set, to eliminate this challenge. Hence, the actual dice sums are completely irrelevant, and say nothing immediately about our edge in craps. But we will come back to this point, and show later how we can determine our edge once we have proven our dice setting skill.

A random shooter should achieve 16 z-axis controlled outcomes on average for every 36 rolls. Of these passes, four are zero pitches, and four are double pitches. For the curious, observe that three pitches is actually a single pitch in the other direction. With this knowledge we can now ask the million dollar statistical question:

"If I roll the dice a bunch of times and observe a certain number of z-axis controlled shots, what is the probability of this occurring randomly?"

This fancy looking question is really the mathematical equivalent of asking "Is there ample evidence that I am a controlled shooter?"

In our next episode� introducing Pro Test©!

Now that we have a better understanding of the physics of dice control, and the meaning of the current SRR analysis method, we can strive to come up with a better and more accurate statistical model for dice control.

In next month's article, we'll introduce the Pro Test©, the new mathematical model used in Smart Craps to analyze dice control. Pro Test is exactly what the title suggests: a test dice controllers can apply to roll sets to see if they are influencing the dice. Pro Test, since it models the maximum information content of dice control through three different and unique statistical tests, requires far less rolls to develop statistical certainty compared to the SRR method. In experiments with actual dice controllers, 50 to 500 rolls are often more than enough to provide statistical certainty (we'll talk about that term and its meaning more next month). But Pro Test is also more than just a tool to prove whether we're a skilled dice controller: it can be used with Smart Craps to optimize our dice sets, and compute our edge with any bet!

Once again, for those who are curious, you can download the software and read the documentation. Pro Test©, as well as everything we'll cover in this series of articles, is completely and thoroughly presented there. See our web site: www.SmartCraps.com.

Learning about dice control�

Ok� maybe we've raised your curiosity about dice control. Time to buy the book, and make millions, right? Wrong: dice control is a physical skill, very different from the discipline of card counting in blackjack. I tell people that it's a raw physical talent on order of complexity to juggling four balls without errors for many minutes at a time (and not two in each hand, for those who've tried!).

Dice control takes practice. And then, a whole bunch more practice. And then, you have to learn how to transfer that skill into the much more difficult realm of the casino floor. And then you're going to have good days and bad days, when you're "hot" or "cold" (not luck� but days when your dice influence skill is good or bad). If you want to get serious about dice control, be prepared to make a different and much larger time commitment compared to blackjack.

There are a few "hands-on" courses for dice control, the first of which I'd recommend is "Golden Touch Craps" by Frank Scoblete and partners (www.GoldenTouchCraps.com). There are also some good (and bad) books, ranging from general interest to precise details. My favorites are "Get the Edge at Craps" by 'Sharpshooter' (deep with good math coverage), and "The Craps Undergound" by Frank Scoblete (a great dialogue from an experienced dice control and seasoned veteran). There are other great texts, and no insult is meant by their exclusion! Search amazon.com or check your favorite gambling store.

CRAPS FOR PROFIT: HOW TO PROVE THAT THAT YOU CAN GET THE EDGE AT CRAPS

CRAPS FOR PROFIT: HOW TO PROVE THAT THAT YOU CAN GET THE EDGE AT CRAPS

Pro Test: a better dice control metric

By Dan Pronovost

Dan Pronovost is the owner and president of DeepNet Technologies, makers of a wide range of gambling training products and software. Their web sites are: www.HandheldBlackjack.com and www.SmartCraps.com and all products are available for free trial download. Dan is the creator of the new card counting system Speed Count, which is being taught by Henry Tamburin and Frank Scoblete in the Golden Touch Blackjack two day courses: www.GoldenTouchBlackjack.com.

In my craps article in last month's BJI newsletter, I introduced readers to Smart Craps, a new software program and statistical analysis tool for dice controllers in the game of craps. We saw in first article that the seven to rolls ratio (SRR), while somewhat intuitive, is not the best possible measure of dice setting skill. This results from the fact that sevens can be both 'good' and 'bad', meaning that they occur when we both achieve and fail z-axis control. This weakens the statistical utility of SRR for determining player dice setting skill.

Let's take a fresh statistical look at dice control, starting with the basic physics principles described last month.

Z-axis rotation

First and foremost, dice setters are trying to limit the dice rotation to the z-axis. This simply means that neither of the outside numbers shows up in the outcome. Hence, there are 4 times 4 = 16 possible outcomes that succeed in rotating in the Z-axis only. With a hardway set, this means each die outcome is one of: 2, 3, 4 and 5.

Secondly, a good dice setter tries to control the number of face rotations or pitches between the two dice when they do achieve z-axis control. Ideally, the two dice leave their hands in perfect symmetry, and rotate equally in the z-axis, bounce off the floor and back, and land with one of four possible outcomes. With a hardway set, this means one of: 22, 33, 44, or 55.

Thirdly, dice setters attempt to try to limit the number of double pitches when they achieve z-axis control. Ideally, the dice land up together (zero face rotations as noted above), or single pitch (are offset by 90 degrees or one rotation). Eliminating double pitches is useful with some dice sets, such as the hardway set: the only seven sums on the z-axis controlled outcomes occur when the dice double pitch (52, 25, 34 and 43). This can be relevant in different points of the game, such as point cycle rolls.

Thinking in practical terms, how do we know if a throw has stayed on z-axis rotation for any given dice set? Or, how do we know how many face rotations or pitches occurred on those successes? While it is very clear with a hardway dice set, other sets will lead to ambiguous results unless the dice are clearly marked (or colored) and the starting dice set recorded. For the purposes of the Pro Test©, we always use a hardway set, to eliminate this challenge. Hence, the actual dice sums are completely irrelevant, and say nothing immediately about our edge in craps. But we will come back to this point next month, and show later how we can determine our edge once we have proven our dice setting skill.

A random shooter should achieve 16 z-axis controlled outcomes on average for any 36 rolls. Of these passes, four are zero pitches, and four are double pitches. For the curious, observe that three pitches is actually a single pitch in the other direction. With this knowledge we can now ask the million dollar statistical question:

"If I roll the dice a bunch of times and observe a certain number of z-axis controlled shots, what is the probability of this occurring randomly?"

This fancy looking question is really the mathematical equivalent of asking "Is there ample evidence that I am a controlled shooter?"

Pro 1 Test

First, let's call a z-axis controlled throw a Pro 1 Test pass. Hence, with a hardway dice set, a throw is a Pro 1 pass if the one and six don't show up in the outcome, and is a Pro 1 failure otherwise. Now, we can complete a roll set of throws, and record how many times we passed and failed the Pro 1 test (each outcome is either a pass or failure).

Now, if we really are capable of influencing the dice outcomes, then we should be able to record a bunch of throws, and the number of Pro 1 passes should be high enough to provide ample evidence of our skill. But how many passes in how many rolls is enough?

To answer these kinds of questions, mathematicians turn to statistical confidence measures. A mathematician will ask:

"What is the probability of a random shooter achieving that many Pro 1 passes (or more) in some number of throws?"

For our purposes, we'll say that if this percentage is less than or equal to 1%, then there is convincing evidence that our shooter is indeed influencing the dice. This means that only 1 in 100 random shooters would achieve that number of Pro 1 passes (or more).

This all sounds very convincing, but how do we convert a number of rolls and number of Pro 1 passes into a mathematically accurate confidence percentage or score? For this, we turn to a tried and true statistical method, called the Bernoulli trial.

Bernoulli trials

Consider a statistical test (independent of craps) as follows:

• You can perform a test (event), which has either a pass or fail outcome. The fail outcome has probability p, and the pass outcome has probability 1 - p.
• You repeat this test n times, observing k failed outcomes, and n - k passes.
• Question: What is the probability of k (or less) failures?

This kind of statistical test is called a bernoulli trial, and is common fare in any first-year university statistics book or course. Here is the equation for the probability of failing k (or less) events (with probability p of failure each) in n trials:

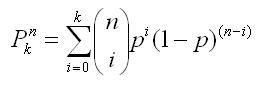
The Bernoulli formula looks simple, but is not the kind of thing that can be computed by hand easily for any sizable 'n' (such as 100 or 500). But it is an easy matter to code this formula on a computer, which is exactly what is done in Smart Craps. When the program displays a Pro Test score, it is simply using the formula above to compute the statistical probability of the observed number of Pro Test passes (or equivalently, failures). When it displays the minimum number of passes required to pass a Pro Test in some number of rolls, it is simply running the Bernoulli equation a bunch of times to determine the number of passes that yields no more than 1% probability.

How does this relate to craps? Suppose a controlled shooter makes n throws with a hardway set, and we see k Pro 1 failures (i.e. n - k Pro 1 passes). Now, we can ask what the probability is of this occurring randomly using truly random dice. If this probability is sufficiently low, then there is a much greater likelihood that the shooter is instead successfully controlling the dice throws than the result being coincidence.

First, we need to determine p, the probability of a six or one (or both) showing up when using a hardway set (i.e. sixes and ones on the outside). The probability of a six or one not showing up on two independent and random dice rolls is 4/6 * 4/6 = 2/3 * 2/3 = 4/9. Therefore, the probability of seeing a six or one show up on either (or both) dice is 1 - 4/9 = 5/9. Hence, p equals 0.5555556 for our craps statistical test.

With this knowledge, we can solve the Bernoulli equation for any particular shooters' Pro 1 test score (probability).

Bernoulli equation from first principles

The Bernoulli equation is very easy to determine from scratch. For those with a mathematical bent, here is the proof (and for those without, please feel free to skip this section):

• Suppose we ask what the probability is of exactly k failures in n trials with probability of failure p.
• There are 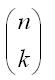(n choose k) possible permutations where we can have exactly k failures, and n - k passes.
• The probability for any one of these events is
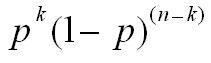
• We can sum the probability of all these events to get the total probability of any exact k failures combination:

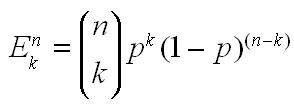
• Hence, the probability of k or less failures in n trials with probability p of failure is simply the sum of the above equations from zero to k (inclusive):

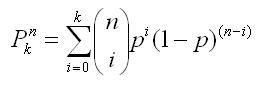
It should be noted that even on a computer, the Bernoulli equation is problematic for n (number of rolls) over 1000. In these cases, the first combinatorial term can quickly overflow the available precision for standard computer math libraries.

To solve this case, Smart Craps uses a standard normal approximation for the probability function when more than 1000 rolls are specified. While not as accurate as the above method, it is always within one roll of the actual exact result (with the Bernoulli equation). Given a desired probability (99%, or 1% by chance), we can solve for the minimum number of Pro Test passes:

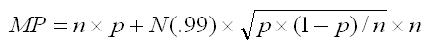
MP = Minimum number of passes required
N(.99) = Normal cumulative distribution function for 99% (N(.99) = 2.326)

Pro 2 Test

The second degree of freedom (or DOF) dice setters attempt to control is the number of face rotations or pitches on their Pro 1 passes (Pro 1 passes, or z-axis control, is the first degree of freedom). Let's call any Pro 1 Test pass that lands with both the dice in sync a Pro 2 Test pass. For example with the hardway set, the results 22, 33, 44 and 55 are Pro 2 passes, while all other results are Pro 2 failures. Notice that all Pro 2 passes are, by default, Pro 1 passes.

Now, we can ask the same question as before:

"What is the probability of a random shooter achieving some number of Pro 2 passes (or more) in some number of throws?"

On the surface, it would seem that we just use the Bernoulli equation again, using [1 - 4/36] = 8/9 for 'p', with 'k' Pro 2 failures in 'n' rolls. There are 4 Pro 2 passes in 36 throws, which means 8/9 probability of a Pro 2 failure.

But statistical tests must be based on a solid knowledge of what they are testing, and how the variables relate. In this case, the hidden wrinkle is that all Pro 2 passes are also Pro 1 passes. Given the physics of dice control, this means all Pro 2 passes are dependent on the Pro 1 passes, which has great meaning in statistical terms. Statistically analyzing the Pro 2 passes without considering the Pro 1 passes, while possible, would lead to questionable results.

To see this, suppose a shooter manages to get 80 Pro 1 passes in 100 rolls, and 20 Pro 2 passes. 20 Pro 2 passes is much more than the statistical average of 4/36 * 100 = 11 in 100 rolls. But, we should also see 4/16=1/4 of our Pro 1 passes be our Pro 2 passes. So, 20 Pro 2 passes in 80 Pro 1 passes is actually statistically average. While showing good z-axis rotation control, the shooter is not managing to get zero pitches more often than expected. Analyzing Pro 2 passes compared to the number of rolls is misleading.

As such, the right statistical question to ask is:

"What is the probability of a random shooter achieving some number of Pro 2 passes (or more) in some number of Pro 1 passes?"

From this point of view, 'p' is the expected number of Pro 2 failures ('k') in 'n' Pro 1 passes. There are 16 expected Pro 1 passes, and 4 Pro 2 passes. This means the probability of a Pro 2 failure ('p') is 1 - 4/16 = 3/4 (75%). Using the Bernoulli equation, we can then come up with the Pro 2 score or probability.

Pro 3 Test

The third degree of freedom dice setters try to minimize is the number of double pitches. A double pitch occurs on a Pro 1 pass where the two dice are rotated by two faces in the outcome. Let's call a double pitch a Pro 3 Test failure. Unlike Pro 1 and Pro 2, we measure failures, rather than passes, with the Pro 3 Test. Hence, dice setters want to maximize their Pro 1 and 2 results, while minimizing their Pro 3 failures. Like Pro 2, all Pro 3 failures are by default Pro 1 passes. The hardway dice set, for example, has these four Pro 3 failures: 25, 52, 34, 43.

In the same way as we did with Pro 2, we can assess the statistical probability of some observed number of Pro 3 failures, using the Bernoulli equation. There are 16 expected Pro 1 passes, and 4 Pro 3 failures. This means the 'p' is 4/16 = 1/4, 'k' is the number of Pro 3 failures, and 'n' is the number of Pro 1 passes.

Pro Test In Practice

So how many test rolls do we need to pass the three Pro Tests? Using the Pro test Solver in Smart Craps, we can easily determine the requirements:

# rolls (n)	Expected # of Pro 1 passes for a random shooter	Minimum # of Pro 1 passes for a 1% probability (n - k)	Pro 1 probability	# of Pro 1 passes as % of # of rolls
100	44 (4/9 of 100)	57	0.78%	57%
200	88	106	0.92%	53%
300	133	154	0.97%	51.33%
400	177	202	0.86%	50.50%
500	222	249	0.92%	49.80%
600	266	296	0.91%	49.33%
700	311	343	0.86%	49.00%
800	355	389	0.97%	48.63%
900	400	436	0.87%	48.44%
1000	444	482	0.93%	48.20%

We are assuming the same 1% pass requirements in the table above as before. In 100 rolls, we only need 13 'extra' Pro 1 passes to yield a 1% pass, 18 in 200, and 21 in 300, etc. From the ratio column, we can see that the challenge of passing the Pro 1 Test gets easier as we add additional rolls. This is not surprising, since the statistical meaning of the results improves as we add more 'events' or rolls. The ratio of Pro 1 passes to number of rolls will approach the expected average of 44.44% (4/9) as the number of rolls increases. It is also equally true that a more skilled dice setter will be able to pass the Pro Test in less rolls than a modest performing shooter.

In tests with actual skilled dice setters, skilled shooters are capable of passing the Pro 1 Test in 100 to 500 rolls, in controlled test conditions. Measuring actual throws in a live casino is not advised, since the shooter most likely will employ dice sets that make recording Pro Test passes difficult. In all Pro Tests, the shooter must use the hardway set, and should record the actual throw as well as the Pro Test pass/failures.

Let's look at the Pro 2 pass requirements:

# of Pro 1 passes	Expected # of Pro 2 passes for a random shooter	Minimum # of Pro 2 passes for a 1% probability (n - k)	Pro 2 probability	# of Pro 2 passes as % of Pro 1 passes
57	14 (1/4 of 57)	23	0.77%	40.35%
106	26	38	0.84%	35.84%
154	38	52	0.92%	33.77%
202	50	66	0.87%	32.67%
249	62	79	0.99%	31.73%
296	74	93	0.75%	31.42%
343	85	106	0.78%	29.15%
389	97	118	0.99%	30.33%
436	109	131	0.97%	30.05%
482	120	144	0.86%	29.88%

We used the minimum Pro 1 pass values as the basis above. Similar to the Pro 1 results, notice that the ratio of Pro 2 passes to Pro 1 passes decreases with increasing sample size, making the Pro 2 Test easier to pass as you add more rolls. The ratio of Pro 2 passes to Pro 1 passes will approach the expected average of 25% (1/4) as the number of rolls (and hence, Pro 1 passes) increases.

What happens if a shooter can pass one Pro Test, but not the others? This is completely acceptable with Pro Test, and Smart Craps allows you to test this. Let's look at different Pro 2 Test results in exactly 200 rolls:

# of Pro 1 passes	Pro 1 probability/pass?	Minimum # of Pro 2 passes for a 1% probability (n - k)	Pro 2 probability
88	57.73%/no	33	0.63%
90	46.43%/no	33	0.93%
92	35.43%/no	34	0.73%
94	25.54%/no	35	0.57%
96	17.33%/no	35	0.83%
98	11.04%/no	36	0.66%
100	6.58%/no	36	0.94%
102	3.67%/no	37	0.75%
104	1.91%/no	38	0.59%
106	0.92%/yes	38	0.84%

Since the Pro 2 pass criterion is dependent on the Pro 1 passes, we need far less Pro 2 passes with low Pro 1 pass results. This may indicate a shooter who is not yet controlling z-axis rotation all that well, but when they do, they manage to keep the dice spinning together very well. In Smart Craps, you can enable and disable any combination of the three Pro tests.

Lastly, let's look at the Pro 3 pass requirements:

# of Pro 1 passes	Expected # of Pro 3 failures for a random shooter	Maximum # of Pro 3 failures for a 1% probability (n - k)	Pro 3 probability	# of Pro 3 failures as % of Pro 1 passes
57	15 (1/4 of 57)	6	0.55%	10.52%
106	27	16	0.97%	15.09%
154	39	25	0.60%	16.23%
202	51	36	0.96%	17.82%
249	63	46	0.90%	18.47%
296	74	56	0.80%	18.92%
343	86	66	0.70%	19.24%
389	98	77	0.91%	19.79%
436	109	87	0.76%	19.95%
482	121	98	0.92%	20.33%

As with the Pro 2 results, notice that the ratio of Pro 3 passes to Pro 1 passes increases with increasing sample size, making the Pro 3 Test easier to pass as you add more rolls. The ratio of Pro 3 passes to Pro 1 passes will approach the expected average of 25% (1/4) as the number of rolls (and hence, Pro 1 passes) increases.

What if I fail the Pro Test?

On the surface, mastering dice control seems easy� just roll the dice a few hundred times, and all you have to do is get about 1/2 of them or more as Pro 1 passes! What can be easier? Well, about 99 out of 100 things�

Remember that the passing metrics for all the Pro Tests is that there is 1% chance or less that a random shooter could replicate the result. This means it is really tough to pass! While looking deceptively easy on the surface, the reality, despite the attractive low pass numbers, is that it is very hard. It takes an incredible amount of practice and time to master the physical skill of dice setting, and even more effort to transfer that skill onto the casino floor and play with an advantage. Learning this skill cannot be done simply by reading books, like blackjack card counting: it takes actual practice throwing the dice, and lots of it!

So what if you fail the Pro Test? Does this mean you are not influencing the dice?

In a word� NO. Failing Pro Test does not mean you can infer the opposite result, that you are not a skilled dice controller.

Pro Test is a one-way test: it only provides statistical certainty that you are influencing dice outcomes. Due to the very high 1% confidence interval requirement for passing, failing, on its own, says very little about your lack of skill. Let's look at some examples.

Suppose you manage to roll 30 Pro 1 passes in 50 rolls. The expected number of passes was 22, so it sure looks like you are throwing in the right direction! But the actual Pro 1 Test score is 1.95%, so you failed the Pro 1 Test (you need 1% or less). But this does not mean that you should hang up your dice and find a new game! 2% as a Pro 1 score is very good, especially in 50 rolls (remember� the ratio of passes to rolls gets easier as you add more throws). Maintaining the same approximate pass ratio in more rolls is usually enough to manage a pass.

Suppose you throw an additional 50 rolls, and get 28 passes. This, by itself, is also a Pro 1 Test failure. But is we combine the results, we get 58 Pro 1 passes in 100 rolls. This is a passing Pro 1 Test result, with a score of 0.4418%� a very healthy pass! There is clear evidence that you are influencing the dice outcomes, in only 100 rolls.

Now, let's look at another example. Suppose you roll 100 rolls, and get 50 passes. The expected number for a random shooter is 44, and the Pro 1 Test score is 15.45%, clearly not a pass. But if we managed to continue with a 50% pass ratio, how many rolls would we need to pass the Pro 1 Test? If we get 250 Pro 1 passes in 500 rolls, the Pro 1 score is 0.7168%, a healthy pass (in fact we pass with 249 or more Pro 1 passes). So, there is good reason to continue and add more throws to the test, to see if you can pass.

But what if you fail miserably, say, 45 passes in 100 throws (a Pro 1 score of 49.4%, which basically indicates a random roll set)? Well, there are no indicators that adding more rolls will help you pass. But what if you simply weren't shooting very well during that test, and your physical skill was not working at its best? Dice control is a tricky talent much like any other skill requiring practice and effort. Dice setters often refer to being 'on' or 'in a rhythm', which is not necessarily voodoo and black magic. You may get good rolls one day, and not the next.

So, suppose the next day the same shooter above tries another 100 rolls, and does get 59 passes. Alone, this is a fantastic Pro 1 pass (0.2408%). Does this mean the shooter is clearly influencing the dice, and ready to make a fortune from the casino?

There is great temptation to exclude recorded roll sets arbitrarily. But if you did so, what would prevent a truly random roller from recording 100 or more 100 throw sessions, until they eventually pass (there is a 1 in 100 chance of a random shooter passing any of the Pro Tests)? For this reason, it is very important to aggregate your recorded Pro Test results, if you want meaningful measures of your skill. In the above case, the shooter actually had 104 Pro 1 passes in 200 rolls, which is Pro 1 score of 1.9069%. As with our first example, this is supporting evidence that the shooter is influencing the dice, but more rolls are necessary. They should practice some more, and roll an additional 100 rolls the next day when they are feeling 'strong'. Suppose they get 52 passes in the next 100 rolls, yielding 156 passes in 300 rolls. This is a Pro 1 score 0.5122%, a clear pass! As with most advantage gambling strategies, diligence, self-control and practice will help you become a better player.

What if I passed some of the Pro Tests, and fail others?

Even extremely proficient dice controllers will find that it is very difficult to pass all three Pro Tests. From actual experimental results, those who pass tend to only pass Pro 1, or pass Pro 1 and only one of the other two. Also, Pro 2 tends to be the hardest test to pass, especially if you pass Pro 1, since you need all the more Pro2 passes (and less Pro 3 failures). For modestly skilled shooters, passing Pro 3 in isolation is the most likely case. Passing even one of the Pro Tests can often be sufficient to get a positive edge on some bets.

Recording your roll sets

You've read the books about dice setting, practiced your throws, maybe taken a course, and now you're ready to see if you're just a chicken feeder (a random shooter), or hot dice controller. Pro Test is clearly the way to answer the question, but how do you go about doing it? Follow these general guidelines for taking the Pro Test:

• Learn the technique and skill: there is no point taking the Pro Test unless you have learned the fundamentals, and practiced. Dice setting is not a skill you can simply experiment with for a few minutes and take a stab at. Passing a Pro test in those conditions is a reflection of luck, and nothing else!
• Practice until it feels right: Do sports stars just hop on the court without warming up? Of course not� and it is no difference for dice setters. From a statistical point of view, it is perfectly acceptable to practice throwing until you feel comfortable and ready to take the test. If you just don't feel 'on', then wait until the next day.
• Get a good test environment: You might think that the best possible conditions for the Pro Test would be a live casino, with all the distractions and challenges of a normal craps table. This is not only impractical, but also incorrect. First off, the Pro Test requires a hardway dice set, so that we can easily determine the Z-axis rotations from the throw result. This is impossible with any different set, such as the 3V, and dice setters will (and should, to maximize their advantage), use different dice sets at different times in a real game. Secondly, the purposes of Pro Test is only to see if a shooter can influence the dice (converting the measured influence to an actual dice edge is covered later). Given the very high 1% confidence interval of Pro Test, it is far better to use ideal experimental conditions. Use of a throwing station in a quiet room is acceptable, as long as you are hitting the back wall most of the time (as one does in a real casino), and the station is similar to a live casino. Furthermore, your test environment (or station) may be worse than an actual craps tables, due to factors such as a bouncy floor on non-level height. So, make sure you give yourself the best possible conditions to throw the dice. Once you pass the Pro Test, Smart Craps uses, by default, a reducing factor (95% confidence interval) on your actual passing ratios to replicate the added challenge of a live casino.
• Get ready to record your throws: Smart Craps includes different recording sheets (Excel, and HTML web browser files) for you to use to record your throws. Stopping after every throw to record the result can be cumbersome and interfere with your ability to pass, so you might want to get a friend to record the throws. Either way, make sure you have an easy way to record your throws accurately.
• Start the test, and record every throw: Decide in advance how many throws you are going to record. You will be biasing the results if you instead simply start recording throws, and stop once you suspect your skill is fading. Choose a low number of rolls, such as 50 or 100, which will not tire you out. Once you start recording rolls, do not exclude any rolls! Doing so would only bias the results, potentially giving you false confidence from the scores.
• Aggregate your prior roll sets: While it may prove helpful to analyze the roll set data alone to determine 'local' trends, you should always sum together your prior recorded roll sets when looking for complete validation of your skill. Long run, you will get generally better Pro Test passing scores as you add more rolls, assuming you are influencing the dice (remember: the Pro Test gets easier to pass as you add more rolls. This is the nature of statistical certainty tests). There are times though when you can safely start excluding roll sets (from a statistical point of view), especially over the long run. For example, your dice setting skill may improve over time, in which case including old roll sets can exert overly negative influence on your scores. Removing all roll sets older than a certain time would be acceptable. Excluding a hodge-podge of roll sets you just didn't like would be unacceptable, and bias the scores.

Summary

Pro Test provides a statistically valid and solid foundation for determining whether a shooter who claims to have dice control skill is in fact influencing the outcomes. The Pro Tests have a 100% correlation to the common physical understanding of dice control (they maximize the information content of dice control, in mathematical terms). By modeling the statistical occurrences of Z-axis rotations, Pro Test is the most accurate possible measure of dice setting and influence. Within a few hundred rolls, good dice setters can state with statistical certainty that they are controlling the dice.

But what about player edge? Next month, we'll see that mathematical modeling of player edge is possible with Pro Test, once again with the help of computer code implemented in Smart Craps.

Optimal Dice Set for Dice Controllers in Craps

Optimal Dice Set for Dice Controllers in Craps

By Dan Pronovost

Dan Pronovost is the owner and president of DeepNet Technologies, makers of a wide range of gambling training products and software. Their web sites are: www.HandheldBlackjack.com and www.SmartCraps.com and all products are available for free trial download. Dan is the creator of the new card counting system Speed Count, which is being taught by Henry Tamburin and Frank Scoblete in the Golden Touch Blackjack two day courses: www.GoldenTouchBlackjack.com.

Introduction

In my craps article in last month's BJI newsletter, I continued introducing readers to Smart Craps, a new software program and statistical analysis tool for dice controllers in the game of craps. We saw in the first article that the seven to rolls ratio (SRR), while somewhat intuitive, is not the best possible measure of dice setting skill. This results from the fact that sevens can be both 'good' and 'bad', meaning that they occur when we both achieve and fail z-axis control. This weakens the statistical utility of SRR for determining player dice setting skill. In the second article, we learned about Pro Test� a new and more powerful statistical analysis tool for analyzing whether you are influencing the dice outcomes.

This month, we'll see that not only can we use Pro Test to determine if we are good dice controllers (instead of just lucky), but also to determine our actual edge in the game, and optimal dice sets. If you haven't yet read the prior two articles, I recommend you do so before continuing below:

• Craps article #1:
www.bjinsider.com/newsletter_62_dice.shtml
• Craps article #2:
www.bjinsider.com/newsletter_63_dice.shtml

Pro Test Player Edge

So� you've practiced your dice control, recorded a few hundred throws, and pass some (or all) of the Pro Tests. Does this mean you're going to make a killing at the casino? What is your player edge (or expectation) on different bets?

While not immediately obvious, it is possible to convert Pro Test results into game expectations. To do so, you need to know:

• The rules of the craps game you are playing in, such as the odds and pay schedule.
• The specific bets you are going to make.
• The dice sets you will use at each point in the throwing cycle.
• Your Pro Test results.

Smart Craps has two ways for you to determine your edge in the game:

1) Exact mathematical analysis for given simple bets (such as pass, or don't pass, with or without odds).

2) Craps game simulation.

Converting Pro Test results to exact player expectation

Normally for a random shooter, each of the 36 dice outcomes has exactly 1 in 36 chance of occurring. For dice setters, the odds will vary for each potential outcome in a predictable manner. Once we have a combination of Pro Test results (a shooter may only pass one or two tests, or possibly all three), these can be converted into specific probabilities for each of the 36 outcomes. Once we have this and the dice sets used at every point in the game, we can determine the probabilities for each dice sum. And with this knowledge, we can determine the actual player edge given a specific betting pattern and game. We can do this mathematically, without empirical simulation.

Suppose a shooter passes all three Pro Tests with results p1, p2 and p3 in n rolls (this analysis can be applied similarly if a shooter passes any combination of Pro Tests). For the moment, ignore what the actual dice set is, and think of the outcomes as being in one of the following groups:

1) Pro 1 failures: for any dice set, we know there are 4 * 4 = 16 Pro 1 passing outcomes. Therefore, there are 36 - 16 = 20 possible Pro 1 failure outcomes.

2) Pro 1 passes, excluding Pro 2 and 3: We know there are 16 Pro 1 passes, and 4 each of the Pro 2 passes and Pro 3 failures. This leaves 16 - 8 = 8 Pro 1 passes that are not Pro 2 passes and Pro 3 failures. These are the single pitches (Pro 2 and 3 are zero and double pitches respectively).

3) Pro 2 passes: There are exactly 4 Pro 2 passes of the 16 Pro 1 passes (the hardway results: 22, 33, 44, 55).

4) Pro 3 failures: There are exactly 4 Pro 3 failures (the 'good' seven sums: 25, 52, 34, 43).

For each group above, the outcomes in that group each have the same probability of occurring. For a random throw, this would be exactly 1 in 36. But for a controlled shooter, it will vary.

If a shooter passes the Pro 1 test with a value of p1 in n rolls (such as 57 in 100 throws, in the prior example), then we can assume that the probability of all of the outcomes in the first group is 1 - p1/n. Later, we'll look more closely at this assertion, and add a further conservative confidence interval that weakens the Pro test values, even with a passing result. But for simplicity, we can guess that the shooter's actual talent leads to a probability of Pro 1 failure as noted above. For a random shooter, p1/n is 16/36, so 1 - p1/n = 1 - 16/36 = 5/9 = 55.56%.

For a controlled shooter (say, 57 Pro 1 Passes in 100 rolls), the probability of Pro 1 failure is: 1 - (57/100) = 43/100 = 43.00%. This is significantly less than the random shooter (55.56%, above).

If a shooter passes the Pro 2 test with a value of p2 in p1 Pro 1 passes (such as 23 in 57 Pro 1 passes, as we saw earlier), then the probability of the outcomes in the third group is: (p2/p1)*(p1/n) = p2/n. For a random shooter, p2/n is 4/36 = 1/9 = 11.11%.

For a controlled shooter (say, 23 Pro 2 passes in 57 Pro 1 passes), the probability of all Pro 2 passes is 23/100 = 23.00%. This is significantly higher than the random shooter.

If a shooter passes the Pro 3 test with a value of p3 in p1 Pro 3 failures (such as 6 in 57 Pro 1 passes, as we saw earlier), then the probability of the outcomes in the forth group is: (p3/p1)*(p1/n) = p3/n. For a random shooter, p3/n is 4/36 = 1/9 = 11.11%.

For a controlled shooter (say, 6 Pro 3 failures in 57 Pro 1 passes), the probability of all Pro 3 failures is 6/100 = 6.00%. This is significantly lower than the random shooter.

Now, armed with this approach and a given dice set, we can exactly state the probability of each of the 36 outcomes for a controlled shooter. This is not a simple mathematical operation to complete by hand, by is easy to do with a computer and a bit of code (and this is what Smart Craps does). Then, we can simply sum the probabilities for each unique dice sum (2 to 12), telling us the probability of each roll in craps, for the specified dice set.

If we look at a specific bet, such as a pass line bet, and specify the dice set for each situation (come out roll, 4/10 points, 5/9 points, 6/8 points), we can now come up with an actual player edge. For example, on the come out roll, we know that a 7 or 11 will pay 1 to 1, and 2, 3 and 12 will lose our bet. Each of these four sums will have an exact probability given a dice set and specified Pro test results, as shown above.

Following this approach, it is possible to write a precise equation for the player edge, in terms of the probabilities for each dice sum given a set of specified dice sets. The mathematics is extremely complex and presented separately after this section, but thankfully you don't need to know it� Smart Craps has a built-in edge calculator (in the Dice Set Optimizer) that can turn any Pro Test scores into an exact edge percentage. This is not done via simulation, and is instantaneous! The calculator also accounts for odds (if any), and even allows you to determine the edge for proposition bets such as placing the 6 or 8.

So far the edge calculator sounds pretty good, as long as you know the dice sets that you use for each situation in the game (such as come out roll, and points). But the analysis method above could help us determine the optimal dice sets for any given bet. For each set of Pro Test scores and bet, there will be one (or more) optimal dice sets for the situations that yield the highest possible player edge. Each die can be oriented in one of 24 ways (6 'tops' with four front facings spun around). Hence, there are 24 * 24 = 576 possible dice sets. Many of these are, of course, reflections and rotations of each other, but this does not change the following algorithm for determining the optimal dice sets:

• For each 'situation' (come out roll, 4/10 point, 5/9 point, 6/8 point), do the following:
• Test all 576 dice sets, and see which one contributes the greatest player edge (or least loss). This can be done using the same analysis approach as above, considering only the win and loss outcomes for the situation. For example, on the come out roll, the edge contribution is p7 (probability of a 7 sum) + p11 - p2 - p3 -p12. The remaining outcomes are points, and a similar (but more complicated) equation describes their contribution.
• Of the 576 dice sets, one or more will be optimal, providing the greatest contribution.
• Take the best dice sets for each situation, and re-compute the actual player edge (given the Pro Test analysis approach noted previously).

Once again, we can see that computing optimal dice sets by hand is not possible. But a computer can do it trivially, which is what the Dice Set Optimizer does in Smart Craps. It runs through these calculations for you, telling you instantly the optimal dice sets given your Pro Test values and bets.

Craps simulation

The edge calculator and Dice Set Optimizer are great for simple bets and games, but the real world of craps is filled with twists and variation. What about unusual bets, such as vig or don't bets? What if you bet occasionally on random shooters? What if you vary the size of your bets according to a 'system'? While the edge calculators in Smart Craps are great starting tools, modeling more complex and realistic game situations quickly gets beyond the mathematical approaches described so far.

This is where the craps simulator comes in. In Smart Craps, you can completely describe every aspect of the game, including shooters, frequency of play, game rules, pay schedule, betting systems, SRR shooters, random shooters, Pro test shooters, etc. Then, run a few million (or more) rounds of craps, and see what the empirical results say. Each simulation ends in an exhaustive report file that contains virtually every possible statistic imaginable, including player edge of course.

Summary

Pro Test, the Dice Set Optimizer, and the simulator in Smart Craps, are the essential missing links that dice controllers need to answer the universal gambling question: How much money can I make?

Mathematical Derivation of Edge for Pro Test

For the technically minded folks out there, we also have a complete mathematical derivation and proof of the equations used to compute the player edge in Smart Craps (given a dice set and resulting probabilities for each sum). We are providing this derivation and equations for public peer review, in the interest of openness and fairness. If you're going to trust Smart Craps to tell you your edge at the game, it's only fair to expect the underlying mathematics to be available for review.

The complete presentation on Pro Test, edge calculation, and mathematical formulas is freely available in PDF format at:

www.smartcraps.com/SmartCraps_theory.pdf

Near the end is the mathematical derivation and edge equations. This section provides a mathematical derivation and proof for how the edge calculator works in Smart Craps.